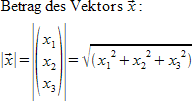
Der Betrag ist allgmein definiert als der Abstand von 0. (vgl. eindimensionaler Zahlenstrahl)
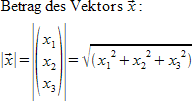
"Betrag des Vektors" vec x ":" newline
lline vec x rline = left lline left ( matrix{x_1##x_2##x_3} right ) right rline = sqrt({x_1}^2 + {x_2}^2 + {x_3}^2 )

""%varphi = %winkel vec a, vec b newline
""vec a cdot vec b = lline vec a rline cdot lline vec b rline cdot cos(%varphi) newline
""vec a cdot vec b = a_1 b_1 + a_2 b_2 + a_3 b_3 newline
""underline "Sätze:" newline
"1."~vec a cdot vec b = vec b cdot vec a newline
"2."~(r cdot vec a) cdot vec b = r cdot ( vec a cdot vec b) newline
"3."~(vec a + vec b) cdot vec c = vec a vec c + vec b vec c newline
"4."~vec a cdot vec a > 0 ~dlrarrow~ vec a <> 0 newline
"5."~(vec a + vec b)^2 = {vec a}^2 + 2 vec a vec b + {vec b}^2

"g:"~vec x = vec p + r vec q newline "Stützvektor" vec p newline "Parameter" r newline "Richtungsvektor" vec q
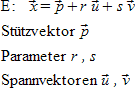
"E:"~vec x = vec p + r vec u + s vec v newline "Stützvektor" vec p newline "Parameter" r, s newline "Spannvektoren" vec u, vec v
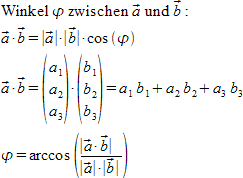
"Winkel" %varphi "zwischen" vec a "und" vec b":" newline
vec a cdot vec b = lline vec a rline cdot lline vec b rline cdot cos(%varphi) newline
vec a cdot vec b = left ( matrix{a_1##a_2##a_3} right ) cdot left( matrix {b_1##b_2##b_3} right ) = a_1 b_1 + a_2 b_2 + a_3 b_3 newline
%varphi = arccos left( {lline vec a cdot vec b rline} over {lline vec a rline cdot lline vec b rline} right )

""underline "Satz:" ~ vec a "und" vec b "(" vec a <> vec 0 "und" vec b <> vec 0 ")" "sind genau dann orthogonal," newline
""~~~~~~```"wenn das Skalarprodukt null ist." newline
""~~~~~~```""vec a ortho vec b ~dlrarrow~ vec a cdot vec b = 0

"Winkel zwischen Gerade" g "und Gerade" h ":" newline
"g:" ~ vec x = left ( matrix{1##2##3} right ) + r left ( matrix{1##5##-4} right ) newline
"h:" ~ vec x = left ( matrix{3##2##-2} right ) + s left ( matrix {2##-2##3} right ) newline
%winkel g,h = arccos left ( {left lline left ( matrix{1##5##-4} right ) cdot left ( matrix {2##-2##3} right ) right rline} over {left lline left ( matrix{1##5##-4} right ) right rline cdot left lline left ( matrix {2##-2##3} right ) right rline} right ) = arccos left ({ lline 1 cdot 2 + 5 cdot (-2) + (-4) cdot 3 rline } over {sqrt{1^2+5^2+(-4)^2} cdot sqrt{2^2+(-2)^2+3^2}} right ) approx arccos(0,7485) approx 41,54°

"Winkel zwischen Gerade" g "und Ebene" E ":" newline
"g:" ~ vec x = left ( matrix{1##2##3} right ) + r left ( matrix{1##5##-4} right ) newline
"E:" ~ left ( vec x - left ( matrix{3##2##-2} right ) right ) cdot left ( matrix {2##-2##3} right ) = 0 newline
%winkel g,E = bold arcsin left ( {left lline left ( matrix{1##5##-4} right ) cdot left ( matrix {2##-2##3} right ) right rline} over {left lline left ( matrix{1##5##-4} right ) right rline cdot left lline left ( matrix {2##-2##3} right ) right rline} right ) = arcsin left ({ lline 1 cdot 2 + 5 cdot (-2) + (-4) cdot 3 rline } over {sqrt{1^2+5^2+(-4)^2} cdot sqrt{2^2+(-2)^2+3^2}} right ) approx arcsin(0,7485) approx 48,46°
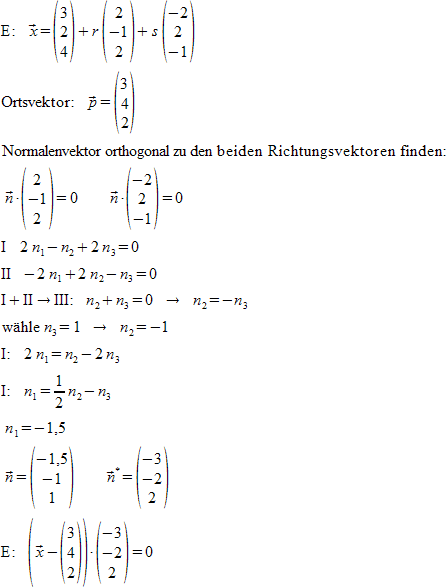
"E:" ~ vec x = left ( matrix{3##2##4} right ) + r left ( matrix{2##-1##2} right ) + s left ( matrix{-2##2##-1} right ) newline
"Ortsvektor:" ~ vec p = left ( matrix{3##4##2} right ) newline
"Normalenvektor orthogonal zu den beiden Richtungsvektoren finden:" newline
""vec n cdot left ( matrix{2##-1##2} right ) = 0 ~~~~ vec n cdot left ( matrix{-2##2##-1} right ) = 0 newline
"I" ~ 2 n_1 - n_2 + 2 n_3 = 0 newline
"II" ~ - 2 n_1 + 2 n_2 - n_3 = 0 newline
"I" + "II" rightarrow "III:"~n_2 + n_3 = 0 ~rightarrow~ n_2=-n_3 newline
"wähle" n_3 = 1 ~ rightarrow ~ n_2 = -1 newline
"I:"~2 n_1 = n_2 - 2 n_3 newline
"I:"~n_1 = 1 over 2 n_2 - n_3 newline
""n_1 = -1,5 newline
""vec n = left ( matrix{-1,5##-1##1} right ) ~~~~ {vec n}^"*" = left ( matrix {-3##-2##2} right ) newline
"E:"~left ( vec x - left ( matrix{3##4##2} right ) right ) cdot left ( matrix {-3##-2##2} right ) = 0
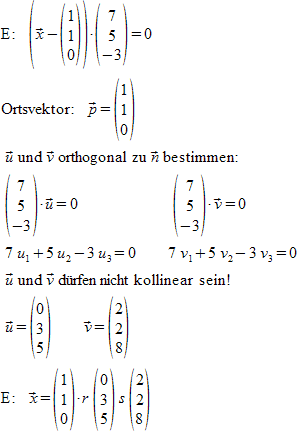
"E:"~left ( vec x - left ( matrix{1##1##0} right ) right ) cdot left ( matrix {7##5##-3} right ) = 0 newline
"Ortsvektor:" ~ vec p = left ( matrix{1##1##0} right ) newline
""vec u "und" vec v "orthogonal zu" vec n "bestimmen:" newline
""left ( matrix {7##5##-3} right ) cdot vec u = 0 ~~~~~~~~~~~~~~
left ( matrix {7##5##-3} right ) cdot vec v = 0 newline
""7 u_1 + 5 u_2 - 3 u_3 = 0 ~~~~
7 v_1 + 5 v_2 - 3 v_3 = 0 newline
""vec u "und" vec v "dürfen nicht kollinear sein!" newline
""vec u = left( matrix{0##3##5} right ) ~~~~
vec v = left( matrix{2##2##8} right ) newline
"E:"~ vec x = left ( matrix{1##1##0} right ) cdot r left ( matrix{0##3##5} right ) s left ( matrix{2##2##8} right )
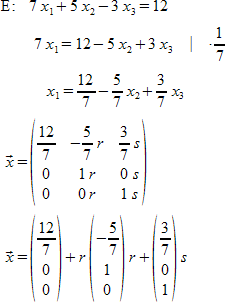
"E:"~ 7 x_1 + 5 x_2 - 3 x_3 = 12 newline
""~~~~ 7 x_1 = 12 - 5 x_2 + 3 x_3 ~~ divides ~~ cdot {1 over 7} newline
""~~~~~~ x_1 = 12 over 7 - 5 over 7 x_2 + 3 over 7 x_3 newline
""vec x = left ( matrix{12 over 7#-{5 over 7} r#3 over 7 s##0#1 r#0 s##0#0 r #1 s} right ) newline
""vec x = left ( matrix {12 over 7##0##0} right ) + r left ( matrix {-{5 over 7}##1##0} right ) r + left ( matrix {3 over 7##0##1} right ) s
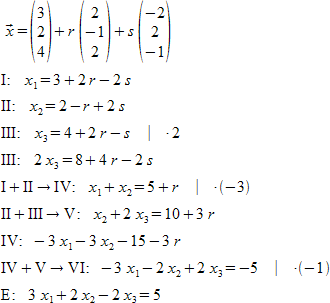
""vec x = left ( matrix {3##2##4} right ) + r left ( matrix {2##-1##2} right ) + s left ( matrix {-2##2##-1} right ) newline
"I:"~ x_1 = 3 + 2 r - 2 s newline
"II:"~ x_2 = 2 - r + 2 s newline
"III:"~ x_3 = 4 + 2 r - s ~~ divides ~~ cdot 2 newline
"III:"~ 2 x_3 = 8 + 4 r - 2 s newline
"I"+"II"rightarrow"IV:" ~ x_1 + x_2 = 5 + r ~~ divides ~~ cdot (-3) newline
"II"+"III"rightarrow"V:" ~ x_2 + 2 x_3 = 10 + 3 r newline
"IV:" ~ -3 x_1 -3 x_2 -15 - 3 r newline
"IV"+"V"rightarrow"VI:"~-3 x_1 - 2 x_2 + 2 x_3 = -5 ~~ divides ~~ cdot (-1) newline
"E:"~ 3 x_1 + 2 x_2 - 2 x_3 = 5
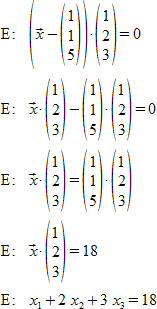
"E:"~ left ( vec x - left ( matrix{1##1##5} right ) right ) cdot left ( matrix {1##2##3} right ) = 0 newline
"E:"~ vec x cdot left ( matrix{1##2##3} right ) -left ( matrix{1##1##5} right ) cdot left ( matrix{1##2##3} right ) = 0 newline
"E:"~ vec x cdot left ( matrix{1##2##3} right ) = left ( matrix{1##1##5} right ) cdot left ( matrix{1##2##3} right ) newline
"E:"~ vec x cdot left ( matrix{1##2##3} right ) = 18 newline
"E:"~ x_1 + 2 x_2 + 3 x_3 = 18
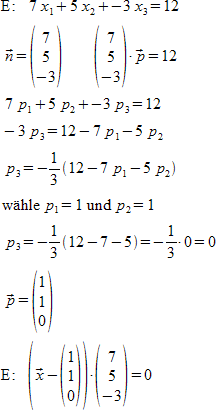
"E:"~ 7 x_1 + 5 x_2 + -3 x_3 = 12 newline
""vec n = left ( matrix{7##5##-3} right ) ~~~~ left ( matrix{7##5##-3} right ) cdot vec p = 12 newline
""7 p_1 + 5 p_2 + -3 p_3 = 12 newline
""- 3 p_3 = 12 - 7 p_1 - 5 p_2 newline
""p_3 = - {1 over 3} (12 - 7 p_1 - 5 p_2) newline
"wähle" p_1 = 1 "und" p_2 = 1 newline
""p_3 = - {1 over 3} (12 - 7 - 5) = -{1 over 3} cdot 0 = 0 newline
""vec p = left ( matrix{1##1##0} right ) newline
"E:"~ left ( vec x - left( matrix{1##1##0} right ) right ) cdot left ( matrix{7##5##-3} right ) = 0
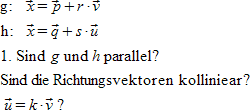
"g:"~vec x = vec p + r cdot vec v newline "h:"~vec x = vec q + s cdot vec u newline "1. Sind" g "und" h "parallel?" newline "Sind die Richtungsvektoren kolliniear?" newline ""vec u = k cdot vec v "?" |
|||
| Ja | Nein | ||
|---|---|---|---|

"Sind" g "und" h "identisch?" newline "Liegt der Punkt" Q "mit dem" newline "Ortsvektor" vec q "auf der Geraden" g "?" newline ""vec q = vec p + r cdot vec v |
"Haben" g "und" h "einen Schnittpunkt?" newline "Hat" vec p + r cdot vec v = vec q + s cdot vec u "eine Lösung?" |
||
| Ja | Nein | Ja | Nein |
|
g und h sind identisch g = h |
""g "und" h "sind parallel und nicht identisch" newline g parallel h ~ and ~ g <> h |
g und h haben einen Schnittpunkt | g und h sind windschief |
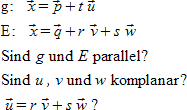
"g:"~vec x = vec p + t vec u newline "E:"~vec x = vec q + r vec v + s vec w newline "Sind" g "und" E "parallel?" newline "Sind" u,v "und" w "komplanar?" newline ""vec u = r vec v + s vec w "?" |
|||
| Ja | Nein | ||
|---|---|---|---|
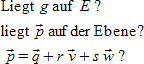
"Liegt" g "auf" E "?" newline "liegt" vec p "auf der Ebene?" newline ""vec p = vec q + r vec v + s vec w "?" |
Es liegt ein Schnittpunkt vor. | ||
| Ja | Nein | Setze g = E und bestimme den Parameter der Geraden. | |
"" g "liegt auf" E "." newline ""g in E |

""g "ist parallel zu" E "und" newline "liegt nicht auf" E "." newline ""g parallel E ~and~ g notin E |
||
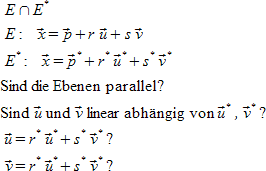
""E intersection E^"*" newline
""E":"~vec x = vec p + r vec u + s vec v newline
""E^"*"":"~vec x = {vec p}^"*" + r^"*" {vec u}^"*" + s^"*" {vec v}^"*" newline
"Sind die Ebenen parallel?" newline
"Sind" vec u "und" vec v "linear abhängig von" {vec u}^"*", {vec v}^"*" "?" newline
""vec u = r^"*" {vec u}^"*" + s^"*" {vec v}^"*" "?" newline
""vec v = r^"*" {vec u}^"*" + s^"*" {vec v}^"*" "?"
|
|||
| Ja | Nein | ||
|---|---|---|---|

"Sind die Ebenen identisch?" newline
"Ist" vec p - {vec p}^"*" "linear abhängig von" vec u, vec v "?" newline
""{vec p}^"*" = vec p + r vec u + s vec v "?"
|
Die Ebenen schneiden sich in einer Geraden | ||
| Ja | Nein |
"Setze" E = E^"*" "und bestimme" newline "die Parameter einer der Ebenen." |
|
"Die Ebenen sind identisch." newline ""E = E^"*" |
"Die Ebenen sind parallel und nicht identisch." newline ""E parallel E^"*" ~and~ E <> E^"*" |
||
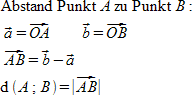
"Abstand Punkt" A "zu Punkt" B ":" newline ""vec a = widevec OA ~~~~ vec b = widevec OB newline ""widevec AB = vec b - vec a newline "d"(A";"B) = lline widevec AB rline
%
%
%
%
%
%
%
%
%
%

""underline "Satz:" ~ "Gegeben sei die Ebene E:"~a x_1 + b x_2 + c x_3 = d "." newline
""~~~~~~```"Dann gilt:" newline
""~~~~~~```"a) "E "geht genau dann durch den Ursprung, wenn" d=0 newline
""~~~~~~```"b) "E "verläuft genau dann parallel zur" x_1 "-Achse (" x_2 "-Achse, " x_3 "-Achse)," newline
""~~~~~~```""~~`"wenn" a = 0 "(" b = 0 "," c = 0 ")" newline
""~~~~~~```"c) "E "schneidet die Koordinatenachsen in den Punkten" newline
""~~~~~~```""~~`S_1(0 mline 0 mline d over a) "," S_2(0 mline 0 mline d over b) " und" S_3(0 mline 0 mline d over c) newline
""~~~~~~```""~~`", wenn" a <> 0 "," b <> 0 "und" c <> 0 "."